1 坐标系与位姿变换

1.1 目标：

理解机器人运动的空间表示，掌握齐次变换矩阵的使用。

1.2 内容：

1.2.1 笛卡尔坐标系：

“机器人的空间视角”

这是人类最直观的理解方式。它基于我们熟悉的直角坐标系，描述的是机器人末端工具中心点 (TCP) 在空间中的位置和方向。

定义： 描述机器人末端相对于基座（Base）或世界（World）的位置和姿态。
数据表示： 通常包含 6 个值：3 个位置值 + 3 个方向值。
- 位置 (Location): X, Y, Z (前后、左右、上下)。
- 姿态 (Orientation): Rx, Ry, Rz (或 A, B, C / W, P, R)，表示绕轴的旋转（如翻滚、俯仰、偏航）。

1.2.2 关节坐标系：

“机器人的内部视角”

这是机器人最原始的控制方式。在这个坐标系下，机器人的每一个位置都是由每个关节的旋转角度（或移动距离）来定义的。

定义： 通过直接控制机器人各个轴（电机）的旋转角度来确定机器人的姿态。
数据表示： 如果是一个六轴机器人，其坐标数据通常表示为一组角度，例如：(J₁, J₂, J₃, J₄, J₅, J₆)。
- 例如：J₁ = 30^∘, J₂ = − 45^∘, …

1.2.3 齐次矩阵（4×4）表示位姿

齐次变换矩阵（Homogeneous Transformation Matrix） 是描述物体在空间中 “位置”和“姿态”最重要的数学工具。

A. 左上角 3 × 3：旋转矩阵 (Rotation)

这一块描述了姿态（Orientation）。
它定义了物体的坐标轴相对于参考系是如何偏转的。
这些数字通常是由欧拉角（Rx, Ry, Rz）计算出来的余弦和正弦值。

B. 右上角 3 × 1：位置向量 (Position / Translation)

这一块描述了位置（Location）。
它非常直观，就是坐标系原点相对于参考系的 X, Y, Z 距离。

C. 最后一行：比例与透视 (Scale & Perspective)

在工业机器人这种“刚体运动”中，物体不会变大变小，也不会发生透视变形。
所以这一行永远是固定的 [0, 0, 0, 1]。它存在的意义主要是为了凑成 4 × 4 的方阵，以便进行矩阵运算。

1.2.4 平移、旋转（欧拉角、四元数）

平移： 主要就是坐标原点的运动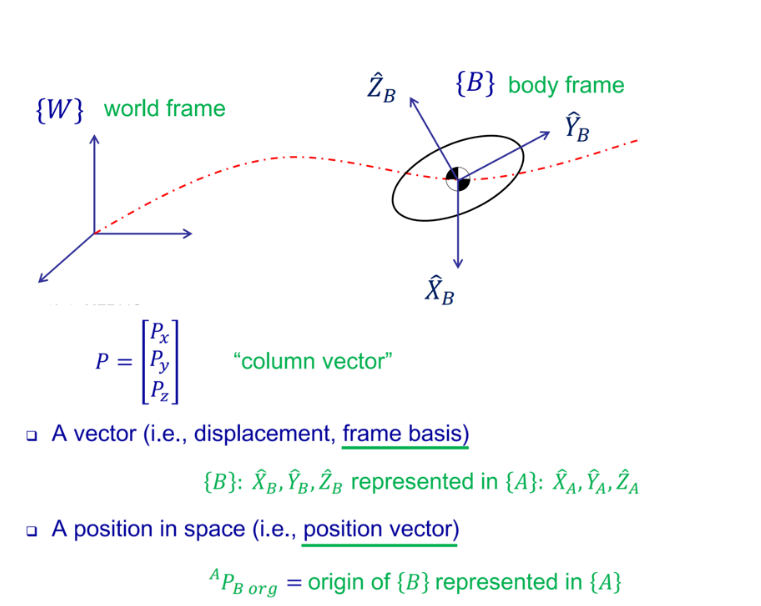

旋转： 1. 右乘： T_new = T_old × R

**物理意义：绕“自身”（当前）的坐标轴旋转** (Intrinsic Rotation)

这是机器人学中最常用的逻辑。

想象你就是那个坐标系（或者机器人末端）：
- 当你已经在空间中处于某个姿态 $T_{old}$ 了。
- 指令是：“绕**你自己的** Z 轴（你的头顶方向）转 90 度”。
- 这时候，旋转矩阵 $R$ 必须**乘在右边**。

**应用场景：**
- **工具操作：** 机器人末端已经伸出去了，现在要让电钻转动，或者让夹具旋转一下。这是相对于**工具本身**的旋转。
- **连杆推导：** 在推导机械臂正运动学（如 DH 参数）时，我们通常是一个关节接一个关节地往后推，这本质上是一连串的右乘（相对于上一关节移动/旋转）。

---

左乘： T_new = R × T_old

物理意义：绕“固定”（世界/基座）的坐标轴旋转 (Extrinsic Rotation)

想象你在玩操纵木偶：
- 木偶在舞台的某个位置 T_old。
- 指令是：“绕舞台中心（世界原点）的 Z 轴转 90 度”。
- 这时候，旋转矩阵 R 必须乘在左边。
- 结果： 整个物体会绕着世界原点画圆弧，发生巨大的位置位移。
应用场景：
- 基座调整： 如果你把整个机器人搬起来，把底座旋转了 30 度。那么机器人末端相对于世界的位置，就是左乘了这个 30 度的变换。
- 坐标系校正： 比如传感器安装歪了，需要在最外层套一个修正矩阵。

欧拉角：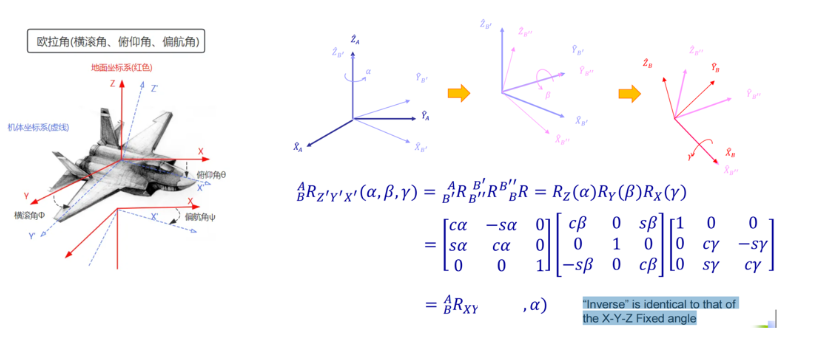

四元数： 比欧拉角多一个自由度。优点是可以避免万向节死锁。

1.2.5 坐标系之间的转换与链式计算

坐标计算可用链式计算进行转换

链式计算举例： 1. World (W): 世界大地（固定不动）。 2. Base (B): 机器人底座（安装在地面上，可能有个偏移）。 3. Flange (F): 机器人末端法兰盘（随关节转动）。 4. Tool (T): 安装在法兰上的夹具（TCP）。

问题： 我控制了关节运动，夹具尖端 (Tool) 在世界 (World) 的哪里？

链式计算公式：

^WT_T = ^WT_B × ^BT_F × ^FT_T

^WT_B (Base Frame): 机械臂装在哪里？（通常是固定的安装误差矩阵）。
^BT_F (Kinematics): 这一项是动态变化的。它是通过 6 个关节角度 (J₁...J₆) 算出来的（正运动学）。
^FT_T (Tool Frame): 夹具有多长？（这是你标定出来的，通常固定不变）。

只要把这三个 4 × 4 矩阵按顺序乘起来，得到的结果 ^WT_T 的最后一列 (x, y, z) 就是夹具尖端的世界坐标。

机器人基础——坐标系与位姿变换(1).docx

1.3 问题：

1.3.1 为什么需要用一个整体的“齐次矩阵”来表示位姿，而不是分开用旋转和位移？

齐次矩阵包含了旋转与位移，同时使用齐次矩阵可以更方便的进行坐标变换。例如需要进行位移或者旋转，只需要将齐次矩阵乘上对应的变换矩阵即可实现变换，引入矩阵乘法，实现相对坐标到实际三位坐标的转换，这有利于运动学正逆解的求解

1.3.2 如果一个点在 A 坐标系下有坐标，我们如何把它转换到 B 坐标系？

求解出A到B的坐标系变换矩阵，求解方法为：然后A坐标系的坐标乘上这个变换矩阵

1.3.3 多个关节坐标系之间的变换，最后是如何得到末端相对基座的位姿的？

通过矩阵链式法则 (Chain Rule) 计算。既然每个关节相对于上一级关节的变换矩阵是已知的（由 DH 参数或关节角度决定），我们只需将这些局部变换矩阵按顺序连乘。公式为：^BaseT_End = ^BaseT₁ × ¹T₂ × … × ^n − 1T_End。最终得到的矩阵，其平移部分和旋转部分即代表末端相对于基座的位姿。

2 轨迹规划

2.1 目标：

理解机器人从起点到终点的运动方式和路径生成。

2.2 内容：

2.2.1 插值方法（直线插值、多项式插值）

插值就是将路径点变得更加密集，如何选择添加原本没有的路径点，需要定义新点坐标与老坐标的关系式。

直线插值 (Linear Interpolation with Parabolic Blends, LSPB)

定义：正如之前讨论的，纯直线会导致无限大加速度。因此工程上采用 LSPB（梯形速度曲线）。
数学描述：这是一个分段函数。设最大加速度为 α，巡航速度为 v。

$加速匀速减速$

这种方法的优点是时间最优（Time-Optimal），因为它尽可能地让电机工作在最大速度限制下。

多项式插值 (Polynomial Interpolation)

定义：使用高阶多项式来拟合轨迹，以获得连续的加速度（甚至加加速度）。
五次多项式 (Quintic Spline)：

为了满足起点和终点的位置 q、速度 q̇、加速度共 6 个边界条件，我们必须使用五次多项式：

q(t) = a₀ + a₁t + a₂t² + a₃t³ + a₄t⁴ + a₅t⁵

通过构建矩阵方程 Ax = b 求解系数 a_i。
- 特点：速度曲线呈钟形（Bell-shaped），比起 LSPB 更加柔顺，减少了机构的冲击，但完成同样动作所需时间通常比 LSPB 长。 >

2.2.2 笛卡尔空间轨迹 vs 关节空间轨迹

关节空间规划 (Joint Space Planning)
- 路径：直接对 θ₁(t), θ₂(t), … 进行插值。
- 数学本质：在构型空间 𝒬 ⊂ ℝⁿ 内寻找路径。
- 优点：计算简单，无奇异点问题。
- 缺点：末端轨迹不可控（通常是乱七八糟的弧线）。
笛卡尔空间规划 (Cartesian Space Planning)
- 路径：规划末端 P(t) = [x(t), y(t), z(t)]^T 为直线或圆弧。
- 数学本质：在任务空间 𝒳 ⊂ SE(3) 内规划，然后通过逆运动学 (IK) 映射回关节空间：
  
  q(t) = f^− 1(x(t))

2.2.3 时间参数化与速度/加速度约束

仅仅画出一条路径（Path）是不够的，我们还需要决定机器人“走多快”，这就是时间参数化 (Time Parameterization)。

设路径几何参数为 s ∈ [0, 1]（0为起点，1为终点）。

轨迹可以表示为复合函数：q(t) = q(s(t))。

我们需要求解 s(t)，使得它满足动力学约束：

速度约束：|q̇_i| ≤ q̇_maxⁱ

根据链式法则：。这意味着路径导数越大，允许的 ṡ（路径速度）就越小。
加速度/力矩约束：|τ_i| ≤ τ_maxⁱ

由动力学方程，必须限制以防止电机力矩饱和。

2.2.4 基本规划算法（RRT、PRM 简介）

PRM (Probabilistic RoadMap)
- 思想：先由“上帝视角”撒点建图，再寻路。
- 步骤：
  1. 在自由空间 𝒬_free 随机撒点 N 个。
  2. 检查两点间连线是否碰撞，若无碰撞则连接，构建图 G(V, E)。
  3. 使用 A* 或 Dijkstra 算法在图中搜索路径。
- 适用：多查询（Multi-query），即地图不变，多次规划不同的起终点。
RRT (Rapidly-exploring Random Tree)
- 思想：像树根一样从起点生长，贪婪地探索未知区域。
- 数学迭代：
  1. 随机采样 q_rand。
  2. 在树上找最近点 q_near。
  3. 向 q_rand 方向生长步长 ϵ 得到 q_new：
- 适用：单查询（Single-query），动态环境，高维机械臂。具身智能基础——机器人轨迹规划.docx

2.3 问题：

2.3.1 为什么在关节空间直线运动和在笛卡尔空间直线运动会产生不同的轨迹？

2.3.2 轨迹规划时，为什么要限制速度和加速度？

这不仅仅是为了“平滑”，而是受限于物理定律和硬件极限。

动力学限制 (Dynamics & Torque Saturation)

请看拉格朗日动力学方程：
- 限制加速度 ()：由第一项可知，力矩 τ 与加速度成正比。如果过大，所需的 τ 会超过电机的额定峰值力矩 τ_peak。一旦超过，电机无法提供足够的力，机器人就会偏离轨道（Tracking Error）。
- 限制速度 (q̇)：由第二项 C(q, q̇)q̇ 可知，科里奥利力和离心力与速度的平方成正比。速度翻倍，非线性干扰力变为 4 倍，这会极大地破坏控制系统的稳定性。
电机物理限制
- 反电动势 (Back-EMF)：直流电机的电压方程 V = IR + K_eq̇。当 q̇ 过高时，反电动势 K_eq̇ 可能会接近电源电压，导致没有电压差来驱动电流 I，电机输出力矩骤降为 0。
机械共振 (Resonance)
- 过大的加速度突变（即加加速度 Jerk）会激发机械臂连杆的低频模态，导致末端剧烈抖动。 ### 2.3.3 如果规定两秒钟必须完成一次动作，应该如何安排轨迹？

3 机器人运动学

3.1 目标：

建立关节运动与末端位姿的数学关系，理解 IK/FK。

3.2 内容：

3.2.1 FK（正运动学）：

已知关节角 → 计算末端位姿

3.2.2 IK（逆运动学）：

已知末端位姿 → 计算关节角

3.2.3 奇异性与冗余度问题

想要快速了解什么是IK FK的同学可以看这个7分钟的短片, 可以对此建立一个粗略的认知：BiliBili 较为简单的过一遍IK和FK的原理可以看这个：CSDN

4-1 逆向运动学引言_哔哩哔哩_bilibili

3.3 问题：

3.3.1 正运动学和逆运动学的输入和输出是什么？

正运动学 (Forward Kinematics):
- 已知所有关节的角度 (J₁…J₆) → 算出末端在空间的坐标 (X, Y, Z)。
- 这是为了让系统知道“我现在在哪”。
逆运动学 (Inverse Kinematics):
- 已知想要去的空间坐标 (X, Y, Z) → 反推出每个关节应该转多少度 (J₁…J₆)。
- 这是为了执行命令，例如“去抓那个工件”。

3.3.2 一个平面两关节机械臂去到同一个目标点，可能会有几种解？为什么？

通常有 2 种解（但在特殊位置只有 1 种或无数种）。

为什么通常是 2 种？（多解性）

这可以用 “手肘朝向” 来直观理解。

想象你的手臂平放在桌面上（平面二连杆）： - 你的肩膀是基座（Base）。 - 你的指尖按在桌上的一个点（目标点）。 - 保持指尖和肩膀不动，你的手肘可以往左凸出去，也可以往右凸出去。

这两个姿态： 1. 肘部向上/左 (Elbow Up/Left) 2. 肘部向下/右 (Elbow Down/Right)

尽管关节角度 (θ₁, θ₂) 完全不同，但末端都到达了同一个坐标 (x, y)。在数学上，这是因为两个圆（以基座为圆心半径 L₁ 的圆，和以目标点为圆心半径 L₂ 的圆）通常有两个交点。

1. 特殊情况（奇异点 Singularity） - 1 种解： 当目标点处于最远边界（手臂完全伸直，L₁ + L₂）或最近边界（手臂完全折叠，|L₁ − L₂|）时。此时两个解重合了。 - 无数种解： 如果 L₁ = L₂ 且目标点刚好在基座原点 (0, 0)。此时第一关节转到任何角度，第二关节只要折叠回来都能回到原点。

3.3.3 如果目标点超出了机械臂的最大工作范围，会怎样？

机械臂逆运动学求解不出到达目标点的姿态，卡死，进入危险区域，可能会导致电机烧毁

4 高阶数学工具：旋量代数

4.1 目标：

理解现代机器人学中的数学工具（李群、李代数）。

4.2 内容：

4.2.1 Twist（螺旋向量）的定义

4.2.2 旋量表示：位姿 = Exponential of a Twist

4.2.3 指数映射与对数映射

4.2.4 应用：利用旋量计算刚体运动、轨迹

4.3 问题：

4.3.1 什么是“斜对称矩阵”？

4.3.2 Twist（螺旋向量）由哪两部分组成？

4.3.3 “刚体位姿等于一个螺旋的指数映射”是什么意思？

5 附录：运动学正逆解应用